动手学深度学习v2 - 卷积

卷积

为什么要使用卷积：分类图片，图片像素大，使用单隐藏层MLP参数过多

两个原则：

• 平移不变性
• 局部性

重新考察全连接层

1. 将输入和输出变形为矩阵（宽，高），之前是一维。

2. 将权重变形维4-D张量（h, w）到（h’, w’），因为需要使每个输入像素都有神经元处理，所以将之前MLP的权重W从2-D变到4-D。

   $$h_{i,j}=\sum_{k,l}w_{i,j,k,l}x_{k,l}=\sum_{a,b}v_{i,j,a,b}x_{i+a,j+b}$$

3. 其中，v是w的重新索引$v_{i,j,a,b}=w_{i,j,i+a,j+b}$，从w到v的转换只是形式的转换，因为在两个四阶张量中，系数之间存在一对一的对应关系。 我们只需重新索引下标 (k, l)，使 k=i+a、l=j+b。

原则1 - 平移不变性

如果出现x的平移导致h的平移（坐标可能发生变化）$h_{i,j}=\sum_{a,b}v_{i,j,a,b}x_{i+a,j+b}$，会导致v发生变化

v（卷积核）不因该依赖于（i，j），不想让v发生变化

解决方案：$v_{i,j,a,b}=v_{a,b}$，即消去i, j这两个维度，(可看作压缩?)

$$h_{i,j}=\sum_{a,b}v_{a,b}x_{i+a,j+b}$$

这就是二维卷积（二维交叉相关）

原则2 - 局部性

$$h_{i,j}=\sum_{a,b}v_{a,b}x_{i+a,j+b}$$

当评估$h_{i,j}$时，我们不因该使用远离$x_{i,j}$的参数

解决方案：当$|a|,|b|>\Delta$时，使得$v_{a,b}=0$

$$h_{i,j}=\sum_{a=-\Delta}^\Delta\sum_{b=-\Delta}^\Delta v_{a,b}x_{i+a,j+b}$$

总结：对全连接层使用平移不变性和局部性得到卷积层

卷积层

二维交叉相关：

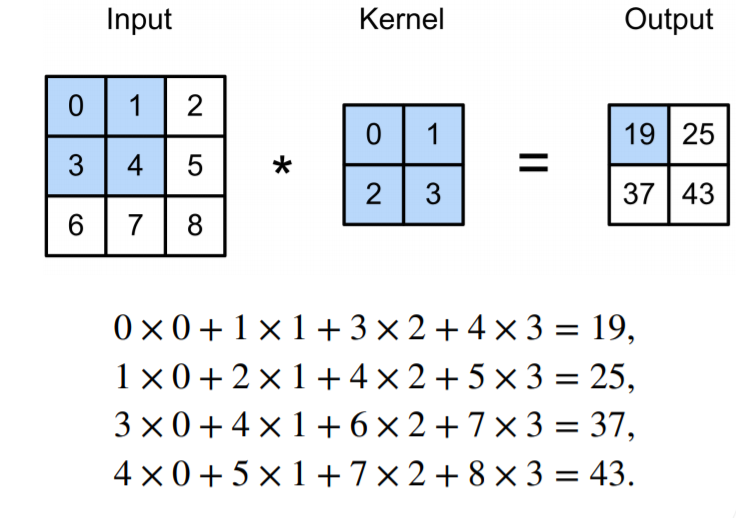
二维卷积层：

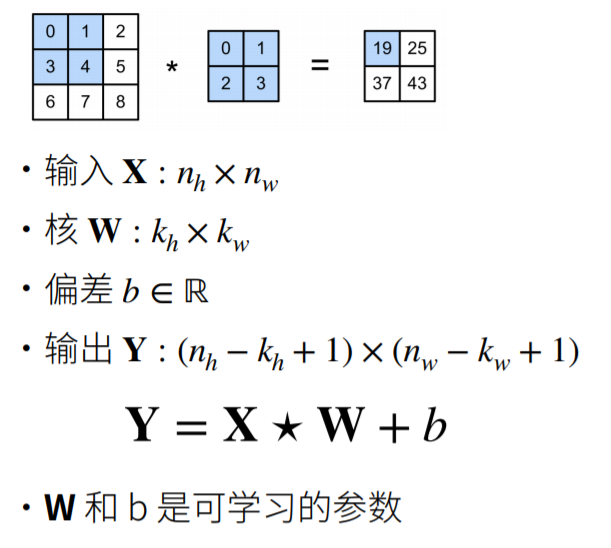
总结：

1. 卷积层将输入和核矩阵进行交叉相关，加上偏移后得到输出
2. 核矩阵和偏移是可学习的参数
3. 核矩阵的大小是超参数，决定局部性

图像卷积实现

互相关运算

def corr2d(X, K):  
    """计算二维互相关运算。"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

实现二维卷积层

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias