动手学深度学习v2 - 多层感知机

感知机

相关定义

给定输入x，权重w，偏移b，感知机输出：

$$o=\sigma \left( \left< w,x \right> +b \right) \,\,\,\,\sigma \left( x \right) =\begin{cases} 1& \text{if }x>0\\ -1& \text{otherwise}\\ \end{cases}$$

类似于二分类问题（输出离散）

不同于回归问题（输出实数），Softmax回归（输出概率，多分类）

其中if的条件为分类错误的情况，对应于感知机的定义

对于上面感知机的损失函数，可以写成：

$$L(w,b) = -y_i(w\cdot x_i+b)$$

当分类正确，即L=0的情况不更新梯度

分类错误时，分别对w，b求偏导：

$$\frac{\partial L(w,b)}{\partial w}=-y_i\cdot x_i$$ $$\frac{\partial L(w,b)}{\partial b}=-y_i$$

进行梯度下降，更新$w=w-y_i\cdot x_i$，以及$b=b-y_i$，和上述一样

感知机参考文献：

https://www.cnblogs.com/chenhuabin/p/11933048.html

XOR问题

感知机不能拟合XOR函数，因为二维输入只能产生线性分割面

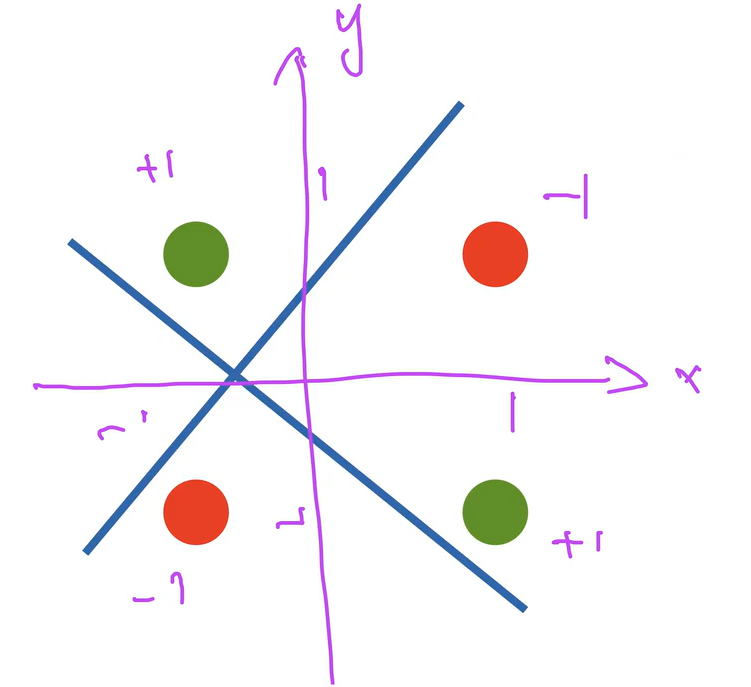
想起了SVM的线性不可分情况

多层感知机

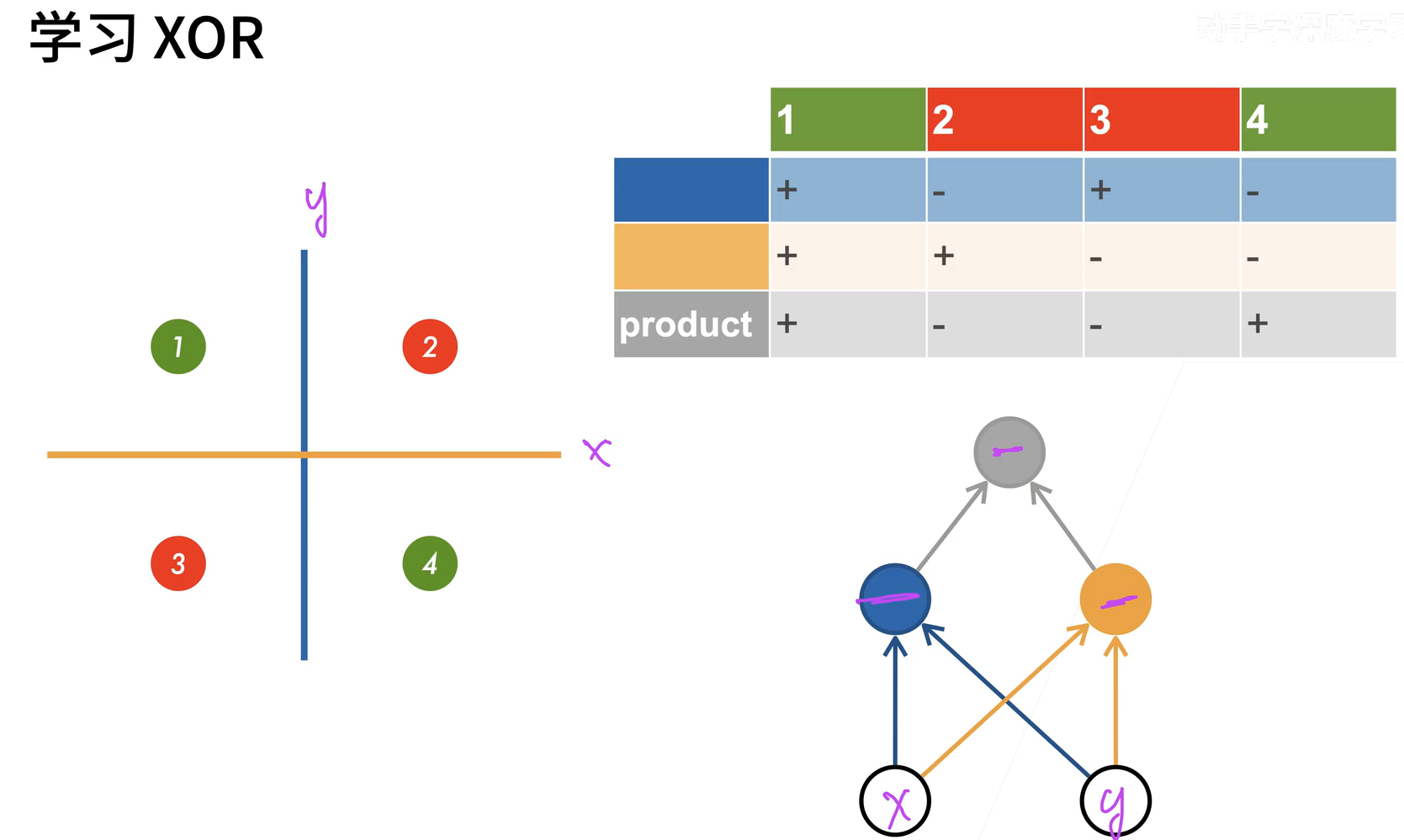
相当于模型使用数据训练两个超平面，再将训练的结果进行XOR运算得到最终的结果，即可以把两类问题分开，可以理解为数字电路的与或门实现异或

单隐藏层

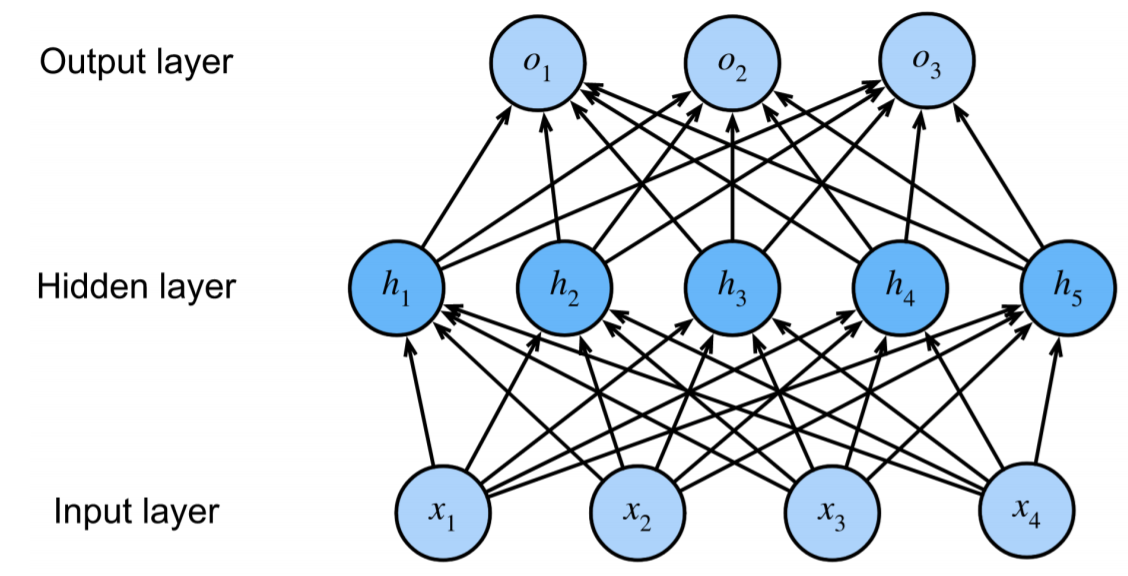
其中，隐藏层的大小为超参数，因为输入输出并不能设置

输入：$x\in R^n$

隐藏层：$W_1\in R^{n\times m}$，$b_1\in R^m$

输出层：$w_2\in R^m$，$b_2\in R$，单分类问题m=1

$$\textbf{w}=\sigma(W_1x+b_1)$$ $$o=w^T_2h+b_2$$

其中，$\sigma$是按元素的激活函数，输出o为标量

Q：为什么需要非线性激活函数

A：假设没有激活函数，输出$o=w_2^TW_1x+b’$，仍然是线性函数

Sigmoid激活函数

不管输入是什么，将输入投影到(0, 1)，比较软，平滑（相较于感知机的$\sigma$函数图像）

$$sigmoid(x)=\frac{1}{1+exp(-x)}$$

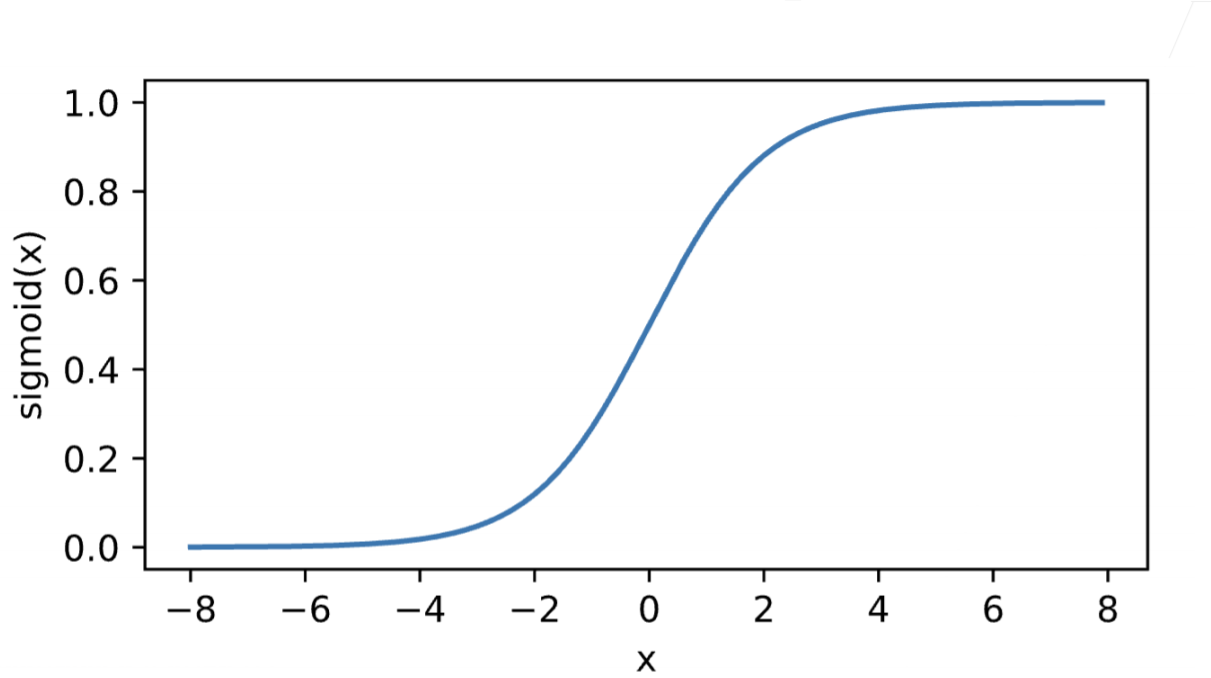
Tanh激活函数

即双曲正切，将输入投影到(-1, 1)

定义：

$$tanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)}$$

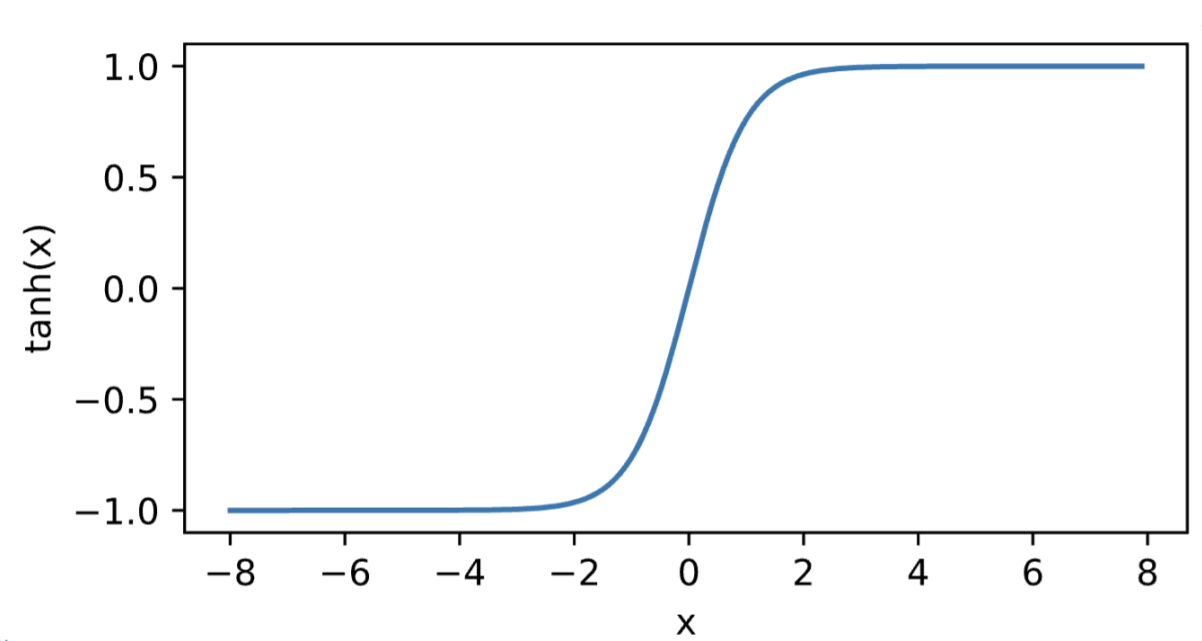
ReLU激活函数

$$ReLU(x)=max(x,0)$$

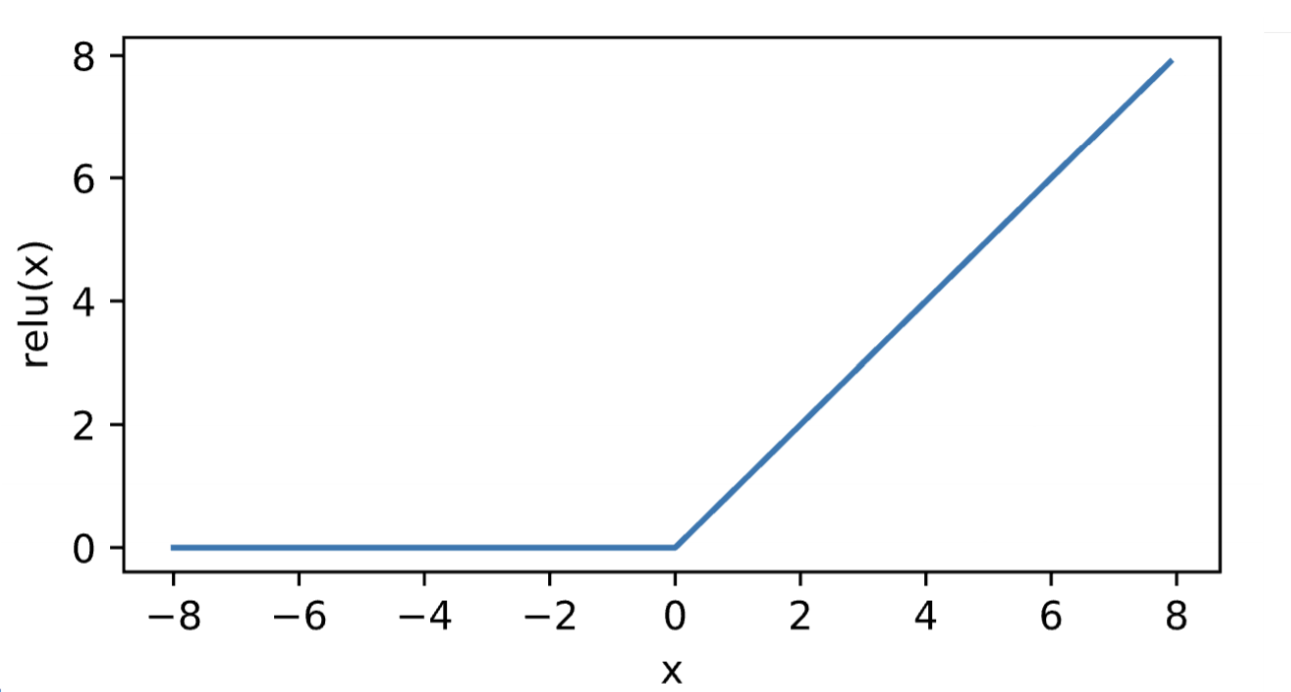
速度快，不需要指数运算

多类问题

$$y_1,y_2,...,y_k=softmax(o_1,o_2,...,o_k)$$

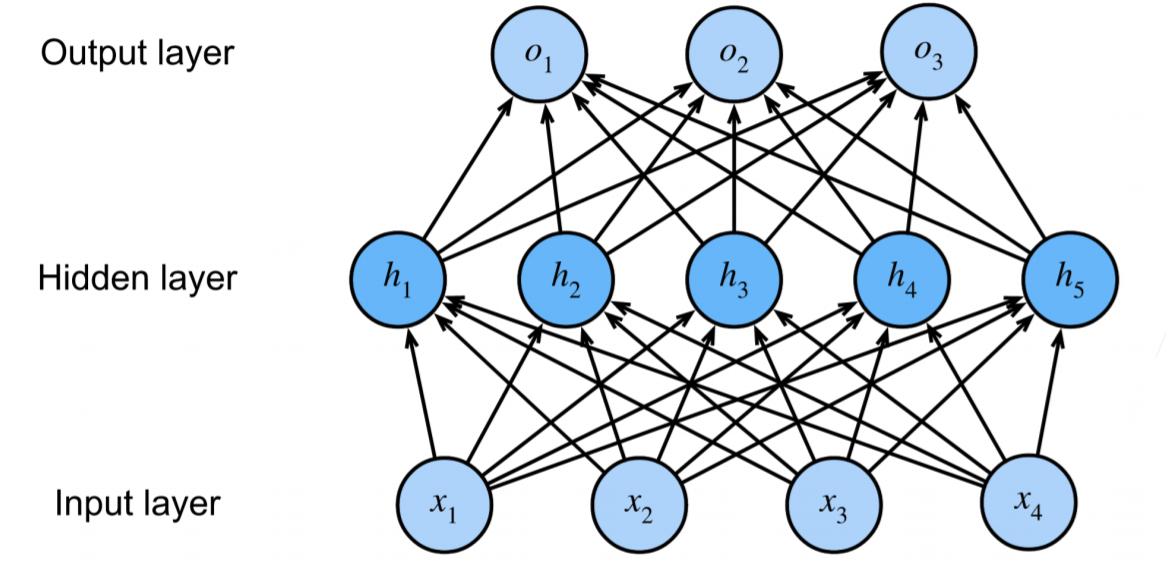
与只有两层的softmax回归不同，加入了隐藏层

输入：$x\in R^n$

隐藏层：$W_1\in R^{n\times m}$，$b_1\in R^m$

输出层：$W_2\in R^{m\times k}$，$b_2\in R^k$

$$\textbf{h}=\sigma(W_1x+b_1)$$ $$\textbf{o}=W^T_2h+b_2$$ $$\textbf{y}=softmax(o)$$

多隐藏层

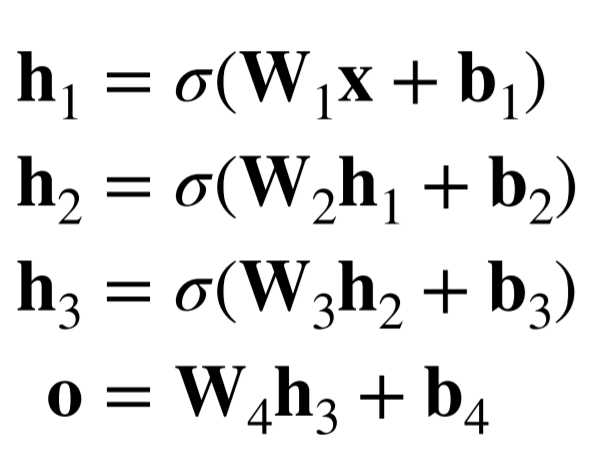
超参数：隐藏层数，每层隐藏层的大小

第一层神经元数量多一点，接下来的层数神经元数量递减（循序渐进）

多层感知机的从零开始实现

初始化输入，隐藏层，输出层

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(
    torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(
    torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

ReLU激活函数

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

模型实现

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X @ W1 + b1)  # 这里“@”代表矩阵乘法
    return (H @ W2 + b2)

loss = nn.CrossEntropyLoss()

多层感知机训练过程与Softmax回归相同

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

多层感知机的简洁实现

初始化各层

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

训练过程

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

模型选择

训练误差：模型在训练数据上的误差

泛化误差：模型在新数据上的误差

泛化误差更重要

训练数据集：训练模型参数

验证数据集：一个用来评估模型好坏的数据集，选择模型超参数，例如将训练数据分割为训练 ，验证数据集

测试数据集：只用一次的数据集，类比考试

K-则交叉验证

将数据分割为K块

for(int i=0;i<k;i++){
    使用第i块作为验证数据集，其余的作为训练数据集
}
报告K个验证集误差的平均

常用K=5, 10

过拟合&欠拟合

模型容量：

拟合各种函数的能力，低容量难拟合训练数据（欠拟合），高容量可以记住所有的训练数据（过拟合）

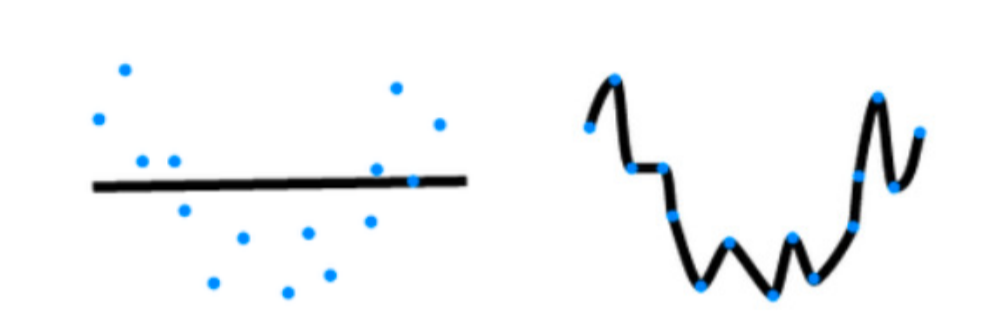
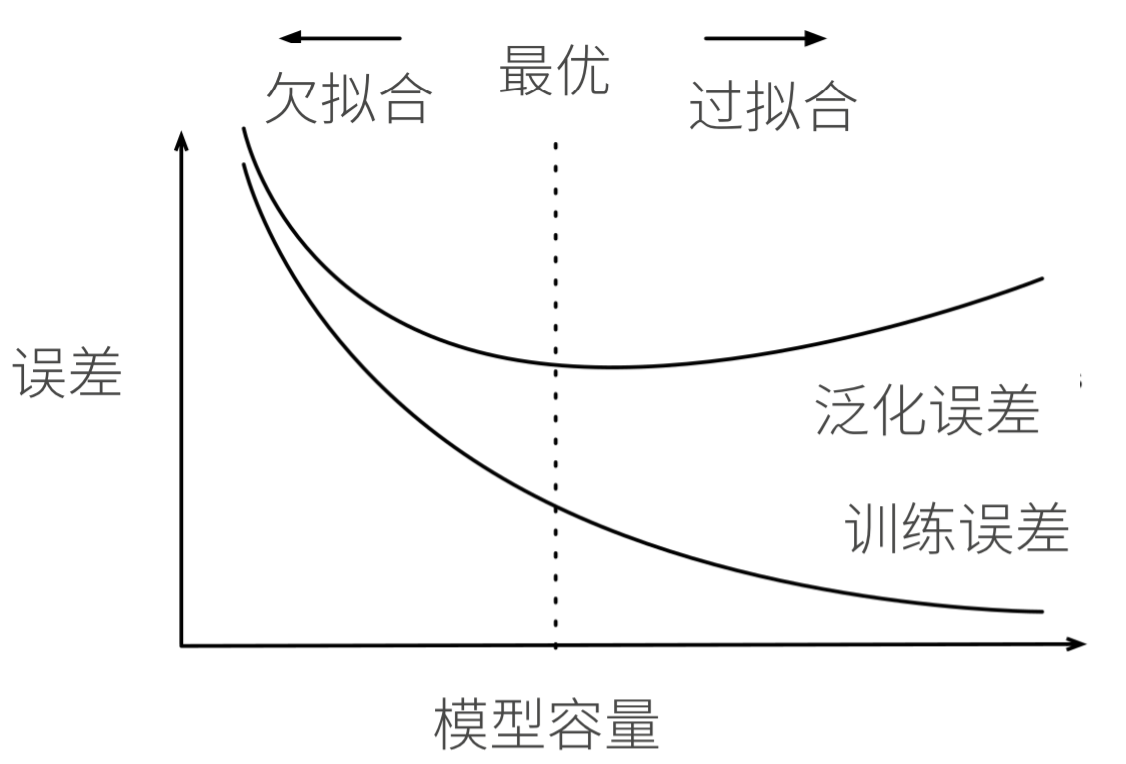
估计模型容量：

难以在不同种类算法之间比较：比如树模型和神经网络

给定一个模型种类，将有两个主要因素：参数的个数，参数值的选择，如图

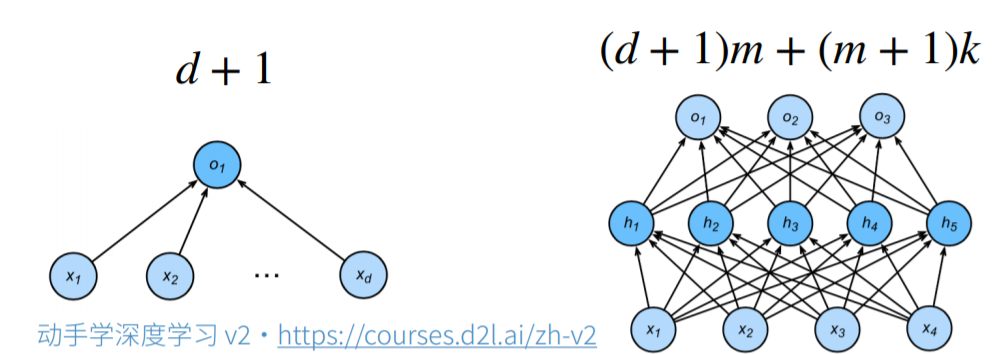
VC维：

对于一个分类模型，VC等于一个最大的数据集的大小，不管如何给定标号，都存在一个模型来对它进行完美分类

线性分类器的VC维：

2维输入的感知机，VC维=3

能够分类任意3个点，不能分类4个点的所有情况（XOR）

支持N维输入的感知机的VC维是$N+1$

一些多层感知机的VC维是$O(Nlog_2N)$

VC维可以衡量训练误差和泛化误差，但是在深度学习中：衡量不是很准确，且计算困难

权重衰退

缓解过拟合

使用均方范数作为硬性限制

通过限制参数值的选择范围来控制模型容量

$$min \ \ l(w,b) \ \ \ \ \text{subject to } ||w||^2\le\theta$$

• 通常不限制偏移b（限不限制差不多）
• 小的$\theta$意味着更强的正则项（指对w的限制更加强，极限法：$\theta=0$,w必须全为0）

不常用

使用均方范数作为柔性限制

对每个$\theta$，都可以找到$\lambda$使得之前的目标函数等价于下面

$$min \ \ l(w,b)+\frac{\lambda}{2}||w||^2$$

超参数$\lambda$控制了正则项的重要程度

• $\lambda=0$，无作用
• $\lambda \rightarrow \infty, w^*\rightarrow 0$

参数更新法则

计算梯度：

$$\frac{\partial}{\partial w}(l(w,b)+\frac{\lambda}{2}||w||^2)=\frac{\partial l(w,b)}{\partial w}+\lambda w$$

时间t更新梯度（梯度下降类似）：

$$w_{t+1}=w_t-\eta \frac{\partial l}{\partial w}=(1-\eta \lambda)w_t-\eta\frac{\partial l(w_t,b_t)}{\partial w_t}$$

通常$\eta\lambda<1$，在深度学习中通常叫做权重衰退

与梯度下降不同的是前面减去了$\eta\lambda w_t$，即减少了权重w，所以是沿着梯度的反方向走了一点

权重衰退通过L2正则项使模型参数不会过大，从而控制模型的复杂度

正则项权重是控制模型复杂度的超参数

丢弃法(Dropout)

原因：一个好的模型需要对输入数据的扰动鲁棒

• 使用有噪音的数据等价于Tikhonov正则，使得权重不会过大（防止过拟合）
• 丢弃法：在层之间加入噪音，可看作一种正则

对x加入噪音得到x’，我们希望最后的期望相同

$$E[x']=x$$

x指的是一层到下一层的输出

丢弃法对每个元素进行如下扰动

$$x_i=\begin{cases} 0& \text{with probability} \ \ p\\ \frac{x_i}{1-p}& \text{otherise} \end{cases}$$

可以看出是一个二项分布，可算出$E(x_i’)=x_i$，实际的效果就是一些元素变为0，一些元素变大

使用丢弃法

通常将丢弃法作用在隐藏全连接层的输出上，即实现随机丢弃隐藏层的一些神经元，被丢弃的神经元权重不会改变，而测试时，不会丢弃神经元

$$h=\sigma(W_1x+b_1)$$ $$h'=dropout(h)$$ $$o=W_2h'+b_2$$ $$y=softmax(o)$$

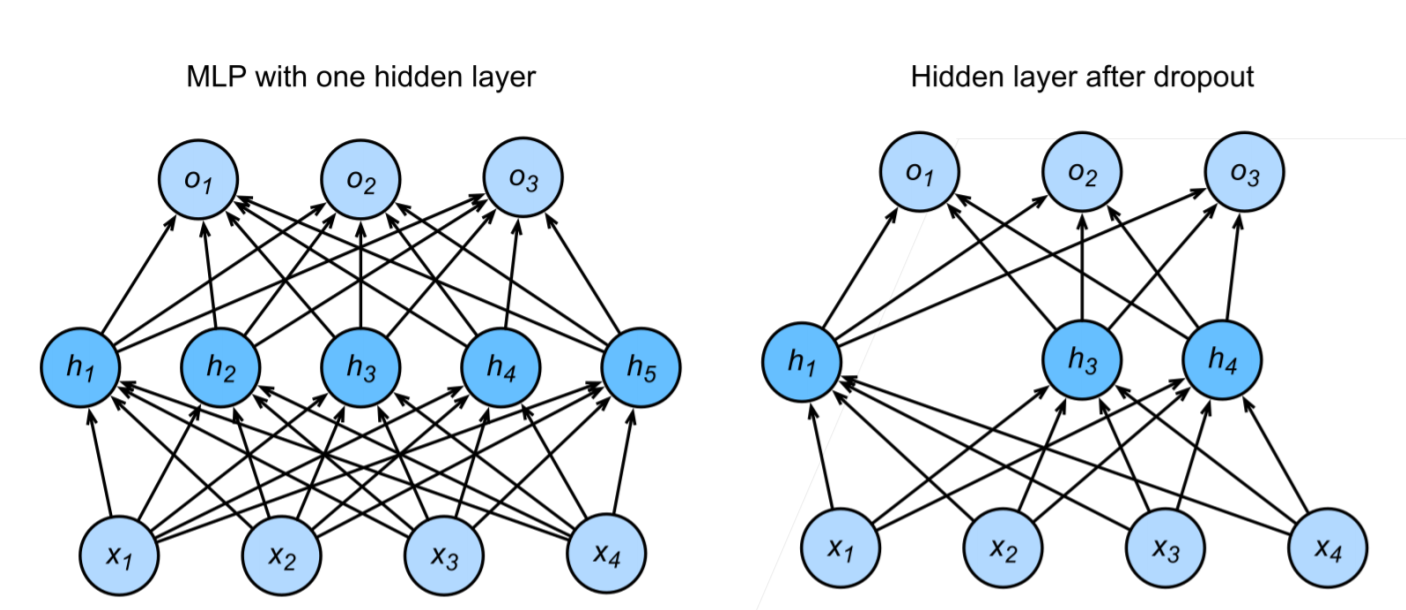
正则项只在训练中使用：他们影响模型参数的更新

在推理过程（测试）中，丢弃法直接返回输入，能保证确定性的输出

总结

• dropout将一些输出项设置0来控制模型复杂度
• 常作用在多层感知机的隐藏层输出上
• 丢弃概率是控制模型复杂度的超参数

代码实现

dropout

def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃。
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留。
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

数值稳定性

计算神经网路的梯度时：

根据链式法则，d层的神经网络需要计算d-t次矩阵乘法

因此带来了两个问题：梯度爆炸，梯度消失

推导：

$$\frac{\partial h^t}{\partial h_{t-1}}=\frac{\partial f_t(h_{t-1})}{\partial h_{t-1}}=diag(\sigma'(W^th^{t-1}))W^t$$

就是雅可比矩阵的推导，再用链式法则，多乘了$W^t$

梯度爆炸

使用ReLU作为激活函数

可以知道ReLU的导数：

$$\sigma'(x)=\begin{cases} 1 &if\ x>0 \\ 0 &otherwise \end{cases}$$

对角矩阵里面主对角线的元素不是0就是1

如果d-t很大，梯度的值会因为$\prod_{i=t}^{d-1}{W^t}$而增大

出现问题：

• 超出值域（inf）

  对于16位浮点数（半精度浮点数）尤为严重（6e-5~6e4）

• 对学习率敏感

  • 如果学习率太大-> 参数值(权重)大->梯度大
  • 学习率太小->训练无进展
  • 需要在训练过程中不断调整学习率

梯度消失

假如使用sigmoid作为激活函数

$$\sigma(x)=\frac{1}{1+e^{-x}} \quad \sigma'(x)=\sigma(x)(1-\sigma(x))$$

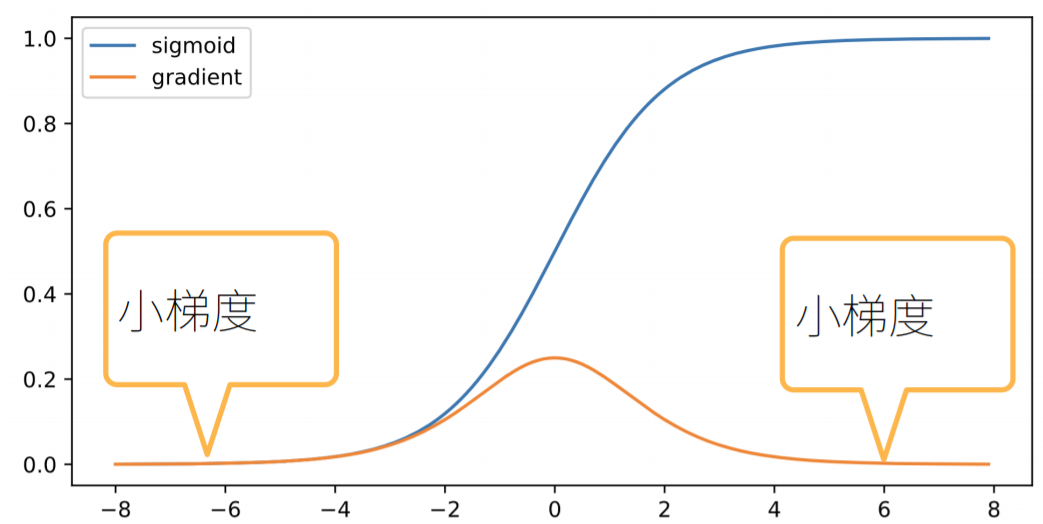
$diag(\sigma’(W^th^{t-1}))W^t$的值当随着权重较大的时候，导数就会变得很小，随着d-t的增大，值就更小了

出现问题：

• 梯度值变为0
  • 对16位浮点数尤为严重
• 训练没有进展
  • 不管如何选择学习率
• 对于底部层尤为严重
  • 仅仅顶部层训练的较好（前几次矩阵乘法可能结果是正常的）
  • 无法让神经网络更深

总结

当数值过大或者过小时会导致数值问题

常发生在深度模型中，因为其会对n个数累乘

让训练更加稳定

目标：让梯度值在合理的范围内

方法：

• 将乘法变加法：ResNet, LSTM
• 归一化，映射到一定的区域
• 梯度裁减，梯度超出范围自动裁减超出范围的部分
• 合理的权重初始和激活函数

让每层的方差是一个常数

• 将每层的输出和梯度都看作随机变量
• 让它们的均值和方差都保持一致（例如：均值为0，方差为一个固定值）

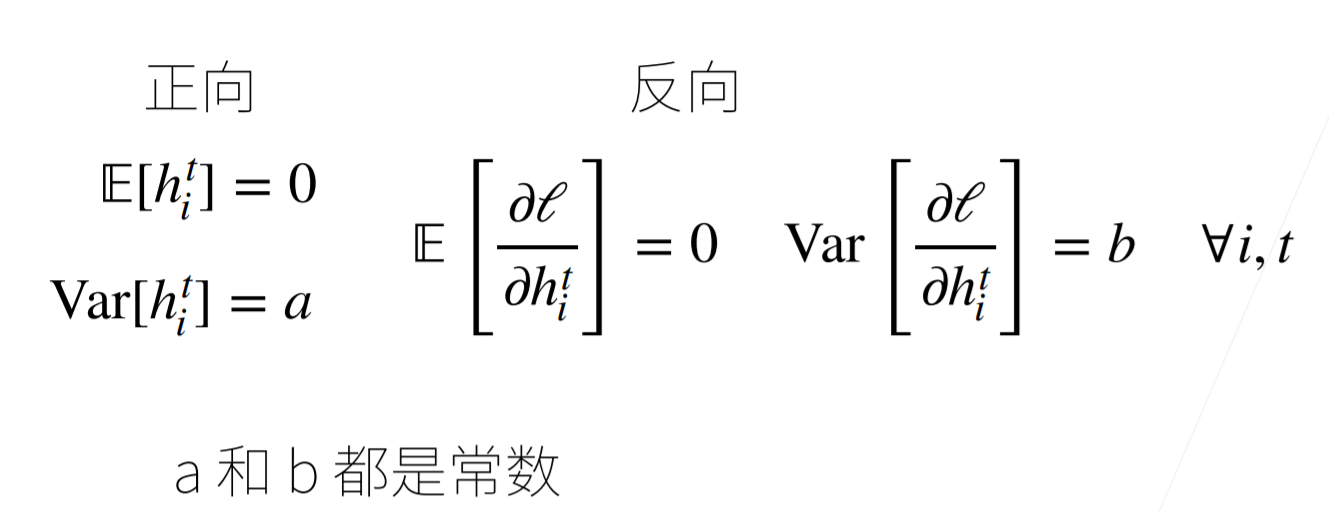
期望为0，即均值为0，Var(方差)

权重初始化

目的：在合理区间里随机初始参数

问题：

• 训练开始时更容易有数值不稳定

  远离最优解的地方损失函数表面可能很复杂

  最优解附近表面会比较平

• 使用N(0, 001)来初始可能对小网络没有问题，但是不能保证深度神经网络

对于MLP：

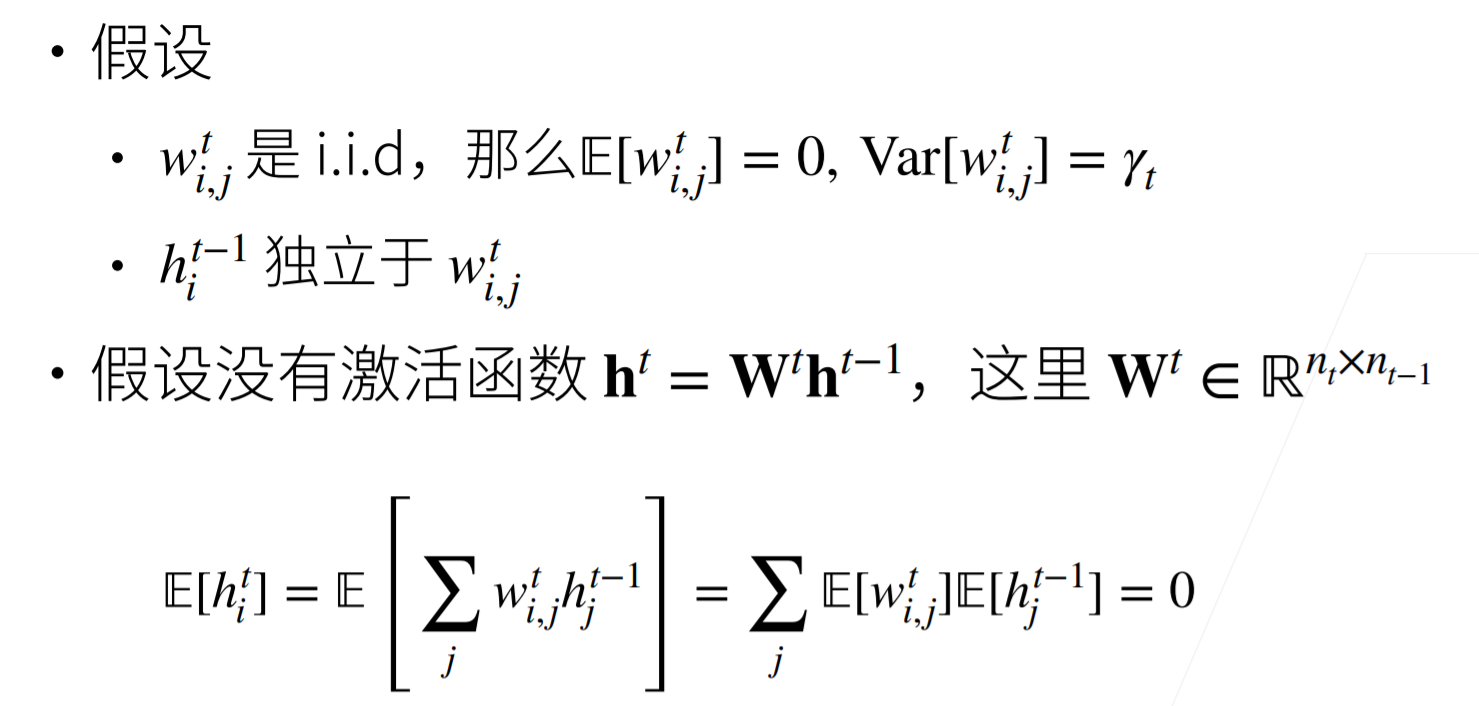
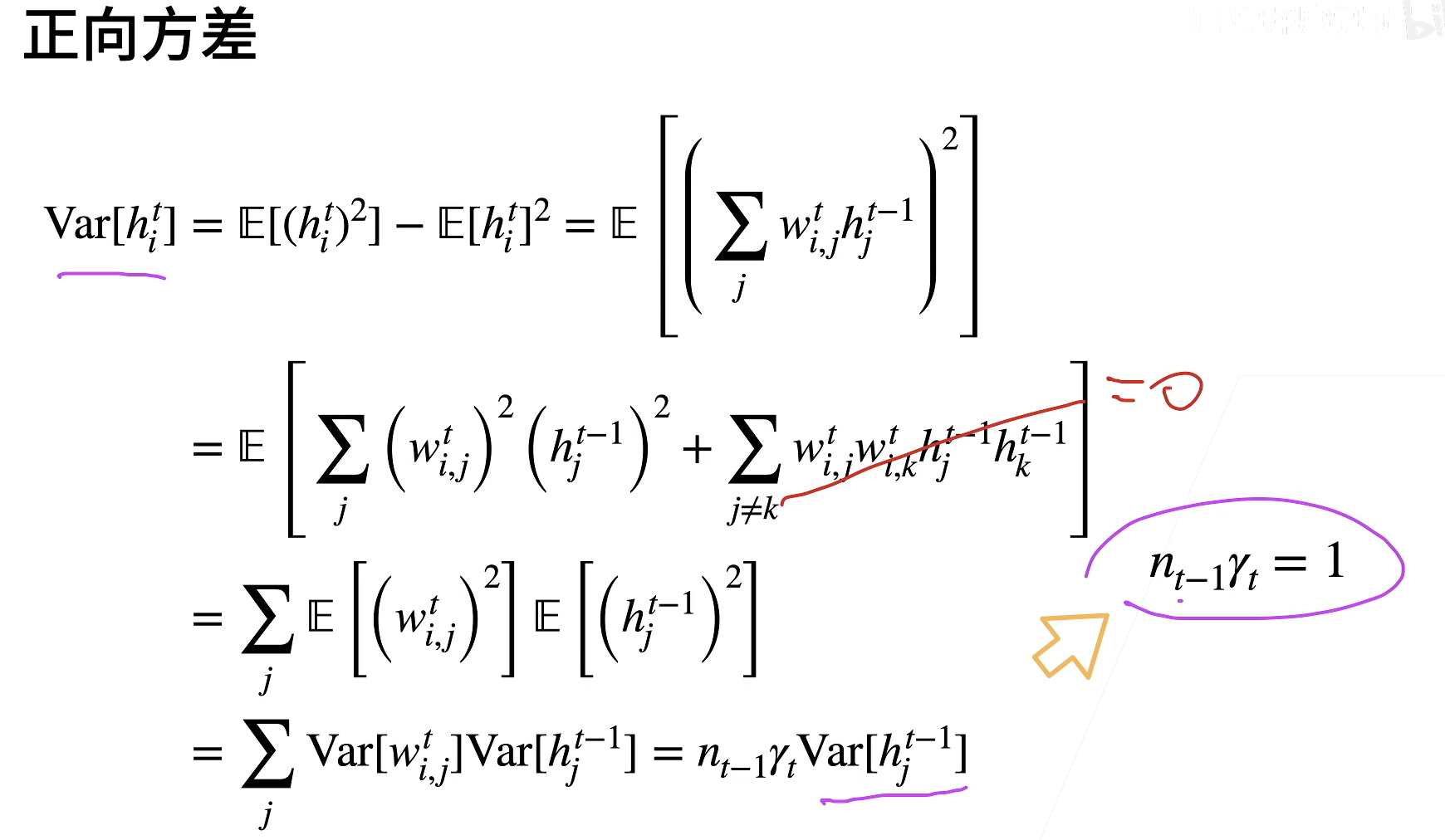
由于$h^{t-1}{i}$独立于$w^t{i,j}$，所以加的项为0，又综合两张图$Var[w^t{i,j}]=\gamma_t$

Xavier初始

因为我们需要满足均值=0，方差相同，需要满足$n_{t-1}\gamma_t=1 \ \& \ n_t\gamma_t=1$，前一项保证前向的方差一致，后一项保证梯度一致，虽然这很难同时满足

可以看出初始化的方差根据输入和输出的维度确定

展开，消去$\beta$项

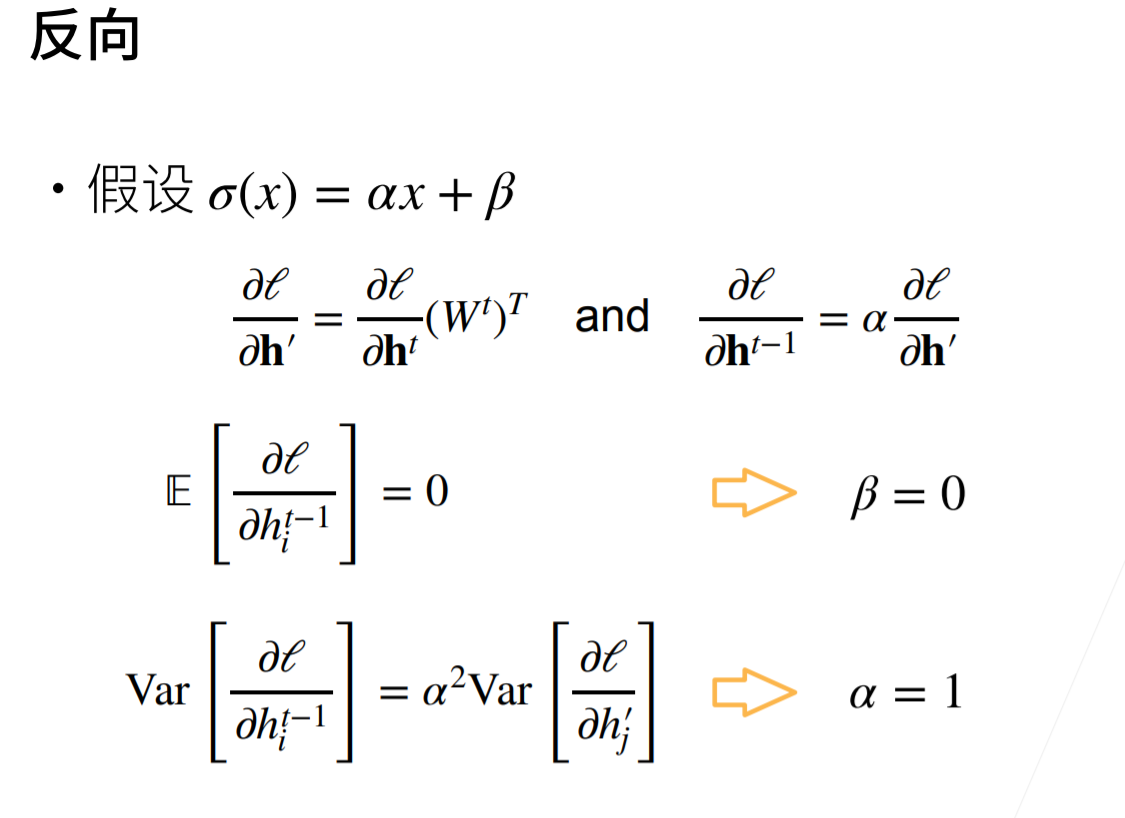
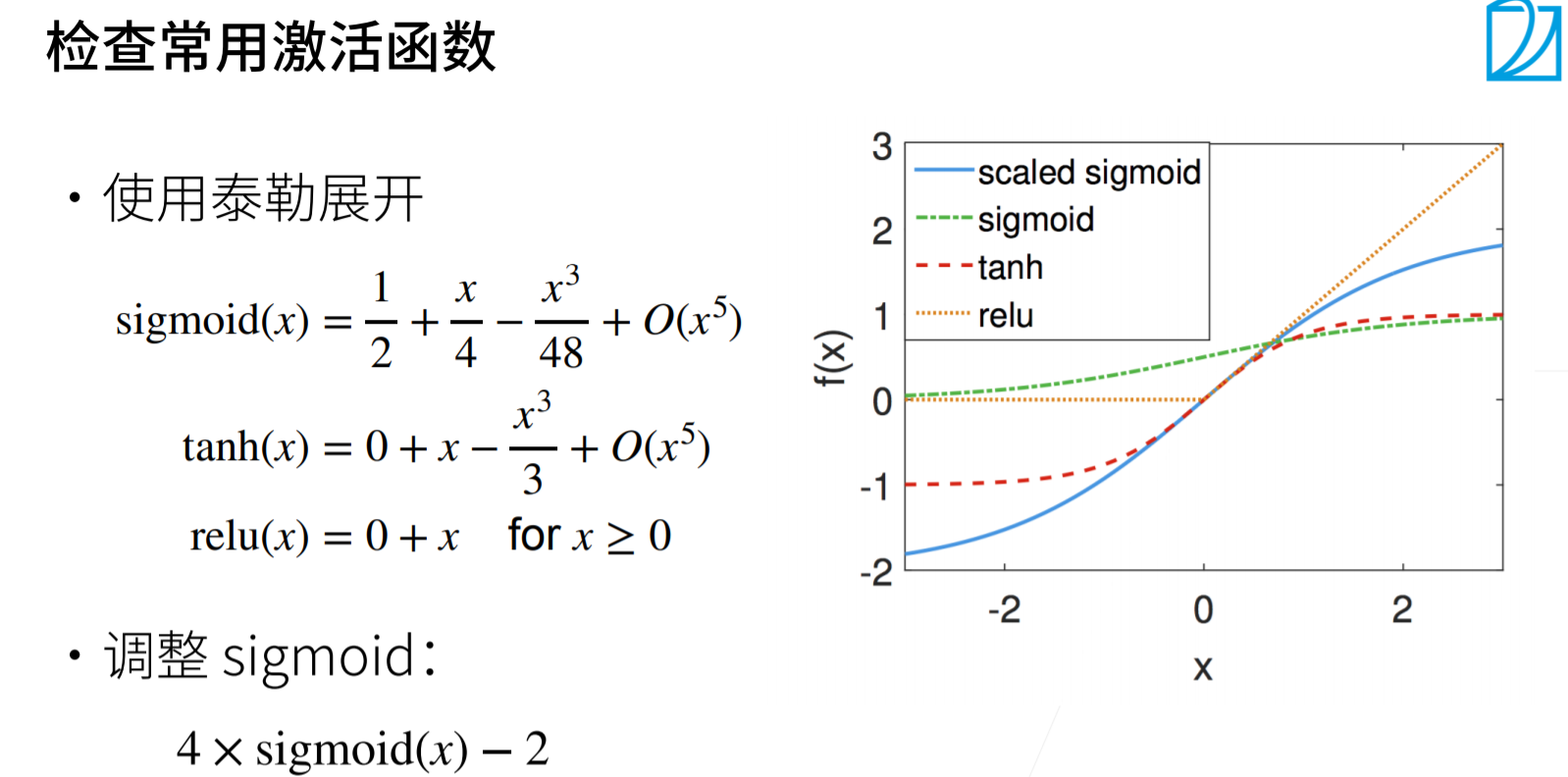
tanh和relu在0点附近可以满足f(x)=x，sigmoid需要调整