动手学深度学习v2 - Softmax回归

Softmax回归

线性回归（回归）：

• 单连续数值输出
• 自然区间R
• 跟真实值的区别作为损失

Softmax回归（分类）：

• 通常为多个输出

• 输出i是预测为第i类的置信度

从回归导多类分类 —— 均方损失：

对类别进行一位有效编码（one-hot）:

$$y=[y_1,y_2,...,y_n]^T \\\\ y_i = \begin{cases} 1& \text{if} \ \ i=y\\ 0& \text{otherwise} \end{cases}$$

使用均方损失

最大值作为预测：$\hat{y}=argmax \ o_i$

需要更置信的识别正确类（大余量）：

$$o_y-o_i \ge \Delta(y,i)$$

指对与正确类的识别远大于非正确类的识别，大于某一阈值（存疑）

将模型的输出作为概率，即输出匹配概率（非负，和为1）：

$$\hat y = \text{softmax}(o) \\$$

其中某一类型的概率

$$\hat{y_i} = \frac{exp(o_i)}{\sum_kexp(o_k)}$$

概率$y$和$\hat y$的区别作为损失

使用exp原因：确保输出为正数且和为1

交叉熵损失

交叉熵用来衡量两个概率（向量）的区别：

$$H(p,q) = \sum_i - p_ilog(q_i)$$

可以把$p_i$理解为$y_i \in {0,1}$，q理解为样本属于i类的概率

将它作为损失：

$$l(y,\hat{y}) = -\sum_iy_ilog\hat{y_i} = -log\hat{y_y}$$

该损失的梯度时真实概率和预测概率的区别：

$$\partial_{o_i} l(y,\hat{y}) = \text{softmax}(o)_i -y_i$$

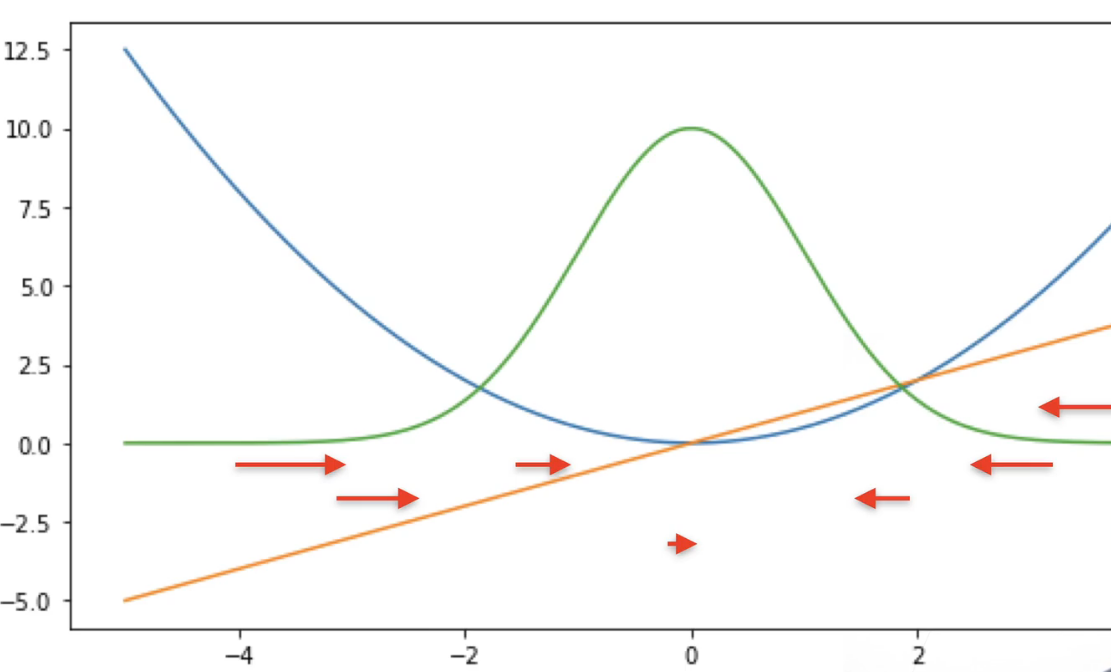
损失函数

L2 Loss

$$l(y,y') = \frac12(y-y')^2$$

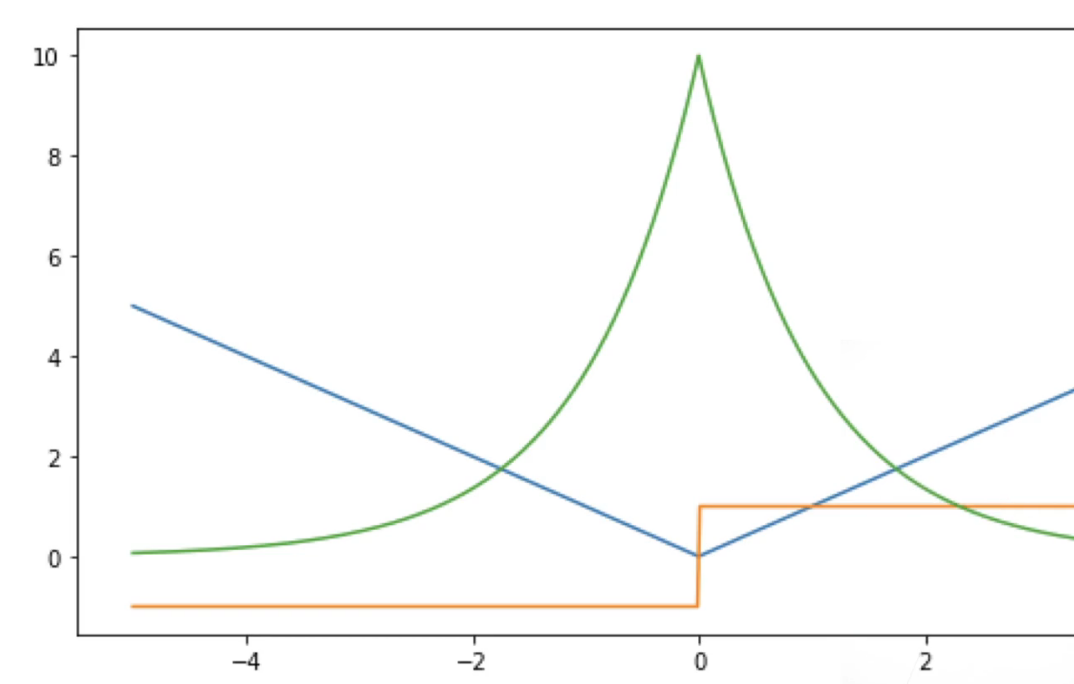
L1 Loss

$$l(y,y') = |y-y'|$$

0点处不可导，0点附近变化大，但是其他地方的梯度为常数稳定

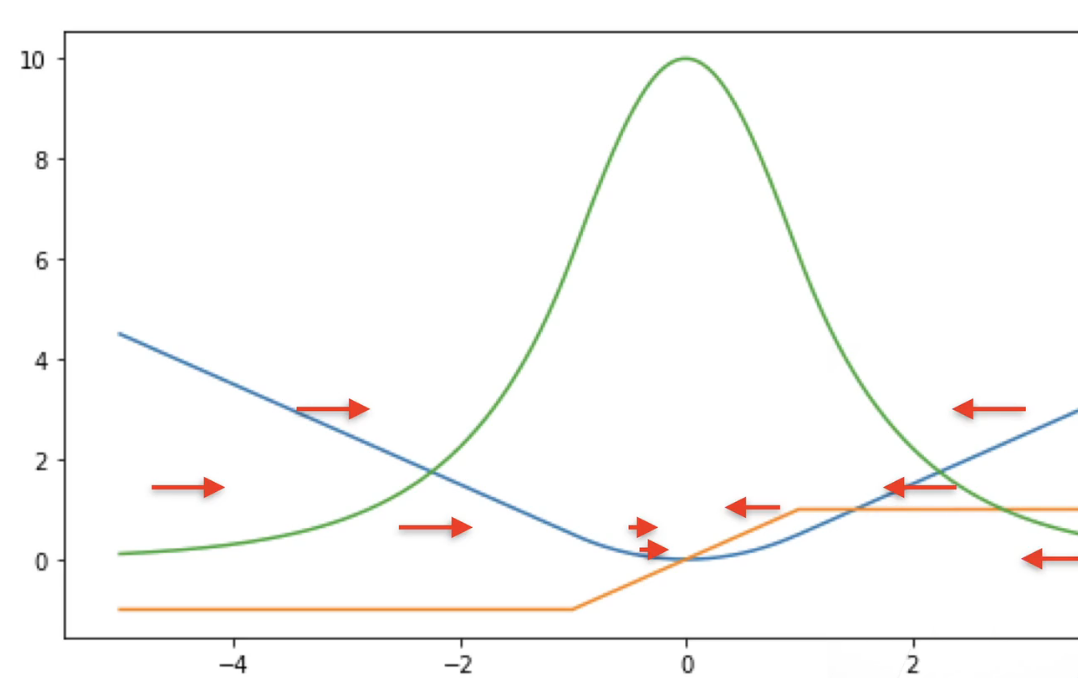
Huber’s Robust Loss

结合L1,L2 Loss

$$l(y,y')=\begin{cases} |y-y'|-\frac12& \text{if} \ \ |y-y'|>1\\ \frac12(y-y')^2& \text{otherwise} \end{cases}$$

当预测值与真实值偏差大时，梯度为常数，稳定

当偏差较小时，梯度的绝对值越小，越平滑

Softmax回归的从零开始实现

导包，读数据

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化w,b

num_inputs = 784 # 图片28*28拉伸成向量
num_outputs = 10 # 10类

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

实现Softmax

def softmax(X):
    X_exp = torch.exp(X) # 对每个元素求exp
    partition = X_exp.sum(1, keepdim=True) # exp相加
    return X_exp / partition # 广播机制 partition复制到与X形状相同，故可以除法获取所有元素的softmax

实现Softmax回归模型

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
# reshape(784, 256)

交叉熵损失函数

def cross_entropy(y_hat, y):
    return -torch.log(y_hat[range(len(y_hat)), y])# 根据真实值y从y_hat中取出y对应分类的概率

cross_entropy(y_hat, y)

计算正确率

def accuracy(y_hat, y):  
    """计算预测正确的数量。"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # 向量大于1行且每行元素大于1
        y_hat = y_hat.argmax(axis=1) # 求出每一行最大值的下标
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

accuracy(y_hat, y) / len(y)

评估任意模型net的准确率

def evaluate_accuracy(net, data_iter):  
    """计算在指定数据集上模型的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval() # 将模型设置为评估模式，不用计算梯度
    metric = Accumulator(2) # 正确预测数，预测总数
    for X, y in data_iter:
        metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

Accumulator 实例中创建了 2 个变量，用于分别存储正确预测的数量和预测的总数量

class Accumulator:  
    """在`n`个变量上累加。"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

evaluate_accuracy(net, test_iter)

Softmax回归的训练

def train_epoch_ch3(net, train_iter, loss, updater):  
    """训练模型一个迭代周期（定义见第3章）。"""
    if isinstance(net, torch.nn.Module): #非手动实现
        net.train()
    metric = Accumulator(3)
    for X, y in train_iter:
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer): # 非手动实现
            updater.zero_grad()
            l.backward()
            updater.step()
            metric.add(
                float(l) * len(y), accuracy(y_hat, y),
                y.size().numel())
        else:
            l.sum().backward()
            updater(X.shape[0]) # sgd
            metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    return metric[0] / metric[2], metric[1] / metric[2]

训练函数

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  
    """训练模型（定义见第3章）。"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc']) # 画图
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,)) # 画图
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

小批量随机梯度下降来优化模型的损失函数

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size) # 前一节函数封装

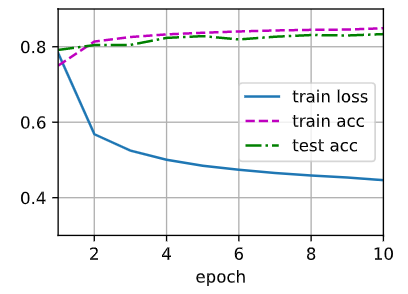
训练模型10个迭代周期

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

对图像进行分类预测

def predict_ch3(net, test_iter, n=6):  
    """预测标签（定义见第3章）。"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true + '\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

Softmax的简洁实现

初始化网络：
因为Pytorch不会隐式地调整输入的形状

因此，需要定义展平层在线性层前调整输入的形状

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

在交叉熵损失函数中传递未归一化的预测，并同时计算softmax及其对数

loss = nn.CrossEntropyLoss()

使用学习率为0.1的小批量随机梯度下降作为优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

训练模型

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)