动手学深度学习v2 - 线性回归

线性模型

给定n维输入 $x = [x_1,x_2,…x_n]^T$

线性模型有一个n维权重和一个标量偏差(offset)

$$w=[w_1,w_2,...w_n]^T, b$$

输出是输入的加权和

$$y=w_1x_1+w_2x_2+...+w_nx_n+b$$

向量版本：$y=\left< w,x \right> +b$

可写成：$y=w^Tx+b$

线性模型可以看作是单层神经网络：输入层$o_1$，输入层为$x_1,x_2,…x_d$

损失函数

比较真实值和预测值的差距，数值越小代表损失越小

设$y$是真实值，$\hat{y}$

平方损失：

$$l(y,\hat{y}) = \frac{1}{2}(y-\hat{y})^2$$

其中$\frac{1}{2}$求导时方便约掉，类似SVM模型的优化目标函数

假设有n个样本，记作：

$\mathbf{X}=[\mathbf{x_1},\mathbf{x_2},…\mathbf{x_n}]^T$，$x_i$为向量，$\mathbf{y}=[y_1,y_2,…y_n]^T$，$y_i$为标量

可以得到训练损失：

$$l\left( \mathbf{X,y,w,}b \right) =\frac{1}{2n}\sum_{i=1}^n{\left( y_i-\left< \mathbf{x}_{\mathbf{i}},\mathbf{w} \right> -b \right) ^2=\frac{1}{2n}\lVert \mathbf{y}-\mathbf{Xw}-b \rVert ^2}$$

最小化损失来学习参数：

$$\mathbf{w^*},\mathbf{b^*}=arg\ min\ l(\mathbf{X},\mathbf{y},\mathbf{w},b)$$

下面忽略向量粗体，需要注意区分，主要是懒，写起来累

显示解

将偏差加入权重，写起来就可以忽略b：

$$X \leftarrow[X,1] \quad w\leftarrow \left[ \begin{array}{} w\\ b \end{array} \right]$$

得到损失函数：

$$l(X,y,w)=\frac{1}{2n}\lVert y-Xw \rVert^2$$

求导（链式法则）得到线性回归的解（解析解）：

$$\frac{\partial}{\partial w}l(X,y,w)=\frac{1}{n}(y-Xw)^TX$$

损失是凸函数，所以最优解满足梯度为0，即：

$$\begin{align} \frac{\partial}{\partial w}l(X,y,w)=0 \\\\ \Leftrightarrow \frac{1}{n}(y-Xw)^TX=0 \\\\ \Leftrightarrow y^TX =w^TX^TX \ \ \ \ \ \ \\\\ \Leftrightarrow w^*=(X^TX)^{-1}X^Ty \\\\ \end{align}$$

基础优化方法

梯度下降

求不出解析解时可以有效训练模型

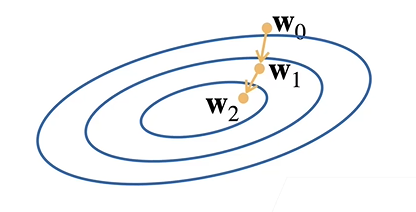
选择一个初始值$w_0$

重复迭代参数t=1,2,3

$$w_t=w_{t-1}-\eta\frac{\partial l}{\partial w_{t-1}}$$

实现过程：沿反梯度方向增加损失函数值（更新参数求解）

$\eta$为学习率：步长的超参数，即沿梯度方向的距离，该参数不能太大也不能太小

小批量随机梯度下降

原因：计算梯度需要遍历整个训练集，慢

只需要随机采样b个样本$i_1,i_2,…,i_b$来计算损失

$$\frac{1}{b}\sum_{i\in I_b}l(x_i,y_i,w)$$

b为批量大小，超参数，不能太大，也不能太小(不利于并行计算)

线性回归的从零开始实现

不使用框架

我们已知w,b的真实值，然后用真实值加上噪声生成数据集，最后用梯度下降拟合出w和b

导包

%matplotlib inline
import random
import torch
from d2l import torch as d2l

生成数据集

def synthetic_data(w, b, num_examples):  
    """
    生成 y = Xw + b + 噪声。
    """
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1)) # y转换为列向量,方便后面随机选取

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

画图

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(),
                labels.detach().numpy(), 1);

随机抽取样本

def data_iter(batch_size, features, labels): #调用一次，随机从样本中抽出10个
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) # 1000
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i +
                                                   batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

定义模型参数

w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

定义模型

def linreg(X, w, b):  
    """线性回归模型。"""
    return torch.matmul(X, w) + b

定义损失函数

def squared_loss(y_hat, y):  
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2 # 此处没有求均值，下面会计算

定义优化算法

def sgd(params, lr, batch_size):  # lr学习率
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size # 更新w,b,求了均值
            param.grad.zero_()

模型训练

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels): #抽10个
        l = loss(net(X, w, b), y) # 求出生成的w,b的loss
        l.sum().backward() # 计算梯度
        sgd([w, b], lr, batch_size)
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels) # 每一个epoch，更新w,b,计算整体数据集的loss
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

估计误差

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

线性回归的简洁实现

准备工作

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

构建一个迭代器来读取样本，有点迷

def load_array(data_arrays, batch_size, is_train=True):  
    """构造一个PyTorch数据迭代器。"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

模型建立

from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

全连接层在 Linear 类中定义，其中in_features=2，即对应x，out_features=1对应y

Sequential 类为串联在一起的多个层定义了一个容器，将数据传入到第一层，然后将第一层的输出作为第二层的输入

初始化模型参数

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

定义损失函数

loss = nn.MSELoss()

定义优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

模型训练

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)
        trainer.zero_grad()
        l.backward()
        trainer.step() # 模型更新，
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')