刘汝佳紫书第七章 - 暴力求解法

本文最后更新于 2021年3月3日 中午

简单枚举法

UVA- 725 除法

输入$n$，求满足$abcde / fghij = n$的不重复的$a…j(a…j \subset 0…9)$，允许前导0

朴素思路：

遍历fghij，从12345~98765

根据n求出abcde

需要注意：当计算出的abcde超过100000，退出

还要判断有没有重复，暴力做法：用一个大小为10的数组存，每次循环计算出每一位，每一位对应数组为1，最后判断数组中是否存在0

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <vector>
#include <list>
#include <fstream>
#define ms(s) memset(s, 0, sizeof(s))

using namespace std;

int main(){
	int n;
	int tt = 0;
	while(cin>>n){
		if(n == 0)
			break;
		if(tt != 0)
			cout<<endl;
		tt++;
		int cnt = 0;
		for(int down=1234;down<100000;down++){
			int up = n*down;
			int tmp[10];
			ms(tmp);
			if(up>=100000){
				continue;
			}
			int u=up;
			int d=down;
			for(int i=0;i<5;i++){
				tmp[u%10] = 1;
				tmp[d%10] = 1;
				u = u/10;
				d = d/10;
			}
			bool flag = 1;
			for(int i=0;i<10;i++){
				if(tmp[i]==0){
					flag = 0;
					break;
				}
			}
			if(flag == 1){
				if(up<10000){
					printf("0%d / %d = %d\n", up, down, n);

				}
				else if(down<10000){
					printf("%d / 0%d = %d\n", up, down, n);
				}
				else
					printf("%d / %d = %d\n", up, down, n);
				cnt++;
			}
		}
		if(cnt == 0){
			printf("There are no solutions for %d.\n", n);
		}
	}
    return 0;
}

坑点：UVA的格式有毒，每个Case间隔一行，最后一个样例只能有1个回车

枚举排列

生成1~n的排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void print_permutation(int n, int *A, int cur){
	if(cur == n){
        for(int i = 0; i < n; i++){
    		write(A[i]);
    		putchar(' ');
        }
        putchar('\n');
    }
    else
    	for(int i = 1; i <= n; i++){
    		int ok = 1;
    		for(int j = 0; j < cur; j++)
    			if(A[j] == i) ok = 0;
    		if(ok){
    			A[cur] = i;
    			print_permutation(n, A, cur+1);
    		}
    	}
}

生成可重集的排列

假如集合中出现重复数字，上面的代码则不适用，会打印多次重复排列

修改上述else部分

1
2
3
4
5
6
7
8
9
10
11
12
else
	for(int i = 0; i < n; i++){
		int c1 = 0, c2 = 0;
		for(int j = 0; j < cur; j++)
			if(A[j] == P[i]) c1++;
        for(int j = 0; j < n; j++)
			if(P[i] == P[j]) c2++;
		if(c1 < c2){
			A[cur] = P[i];
			print_permutation(n, P, A, cur+1);
		}
	}

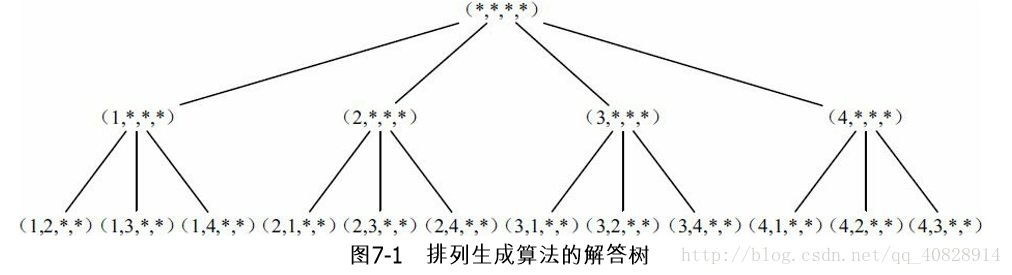
解答树

熟悉递归过程

下一个排列 - C++库函数

1
2
3
#include<algorithm>
//p为待排列集合, n为集合大小
next_permulation(p, p+n)

子集生成

集合没有重复元素

增量构造法

有点迷，搁置一下

1
2
3
4
5
6
7
8
9
void print_subset(int n, int *A, int cur){
	for(int i = 0; i < cur; i++) printf("%d ", A[i]);
	printf("\n");
	int s = cur ? A[cur-1]+1 : 0;
	for(int i = s; i < n; i++){
		A[cur] = i;
		print_subset(n, A, cur+1);
	}
}

位向量法

递归树容易理解

1
2
3
4
5
6
7
8
9
10
11
12
void print_subset(int n, int *A, int cur){
	if(cur == n){
		for(int i = 0; i < cur; i++)
			if(A[i]) printf("%d ", i);
		printf("\n");
		return ;
	}
	A[cur] = 1;
	print_subset(n, A, cur+1);
	A[cur] = 0;
	print_subset(n, A, cur+1);
}

二进制法

最简洁，最好理解

易知：长度为3的集合的子集一共有$2^n$个，位长为3的二进制串即$0\sim2^n-1$也一共有$2^n$个数

1
2
3
4
5
6
7
8
9
10
void print_subset(int n, int s){
	for(int i = 0; i < n; i++)
		if(s&(1<<i)) printf("%d ", i);
	printf("\n");
}

\\调用
int n=3;
for(int i = 0; i < (1<<n); i++)
    print_subset(n, i);

回溯法

N皇后问题

可以转化为全排列问题

每次在一行插入一个皇后，判断其他行的皇后在不在同一条线上

判断主对角线和副对角线上的皇后，看书上图理解

1
cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j]

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void search(int cur){
	if(cur == n)
		tot++;
	else
		for(int i=0;i<n;i++){
			int ok = 1;
			C[cur] = i;
			for(int j=0;j<cur;j++)
				if(C[cur] == C[j] || cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j]){
					ok = 0;
					break;
				}
			if(ok)
				search(cur+1);
		}
}

UVA- 524 Prime Ring Problem

输入$n$，求$1 \sim n$所组成环的排列，要求两两相邻的数字之和为素数

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void dfs(int cur){
    if(cur == n && isPrime(A[0]+A[n-1])){
        for(int i=0;i<n-1;i++)
            cout<<A[i]<<" ";
        cout<<A[n-1];
        cout<<endl;
    }
    else
        for(int i=2;i<=n;i++){
            if(!vis[i] && isPrime(i+A[cur-1])){
                A[cur] = i;
                vis[i] = 1;
                dfs(cur+1);
                vis[i] = 0;
            }
        }
}

调用前要初始化，因为是1开头

1
2
A[0] = 1;
vis[1] = 1;
学习总结
#算法竞赛入门经典 #暴力
刘汝佳紫书第七章 - 暴力求解法
https://nanami.run/2021/01/22/ACM-Algorithm-Chapter7/
作者
Nanami
发布于
2021年1月22日
许可协议